La mecánica es la ciencia que describe y predice las condiciones de reposo o movimiento de los cuerpos bajo la acción de fuerzas. Esto aplicado al ámbito de la ortodoncia, adquiere unas connotaciones particulares, que el clínico debe de conocer.
La práctica clínica nos enseña dos principios fundamentales: primero, que para obtener una respuesta biológica precisa, se deben aplicar estímulos precisos, y segundo, que es necesario el conocimiento de los principios mecánicos que gobiernan las fuerzas, para el control del movimiento dentario.
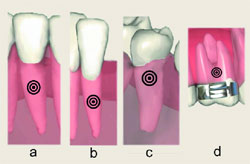 |
| Figura 1. Ubicación del centro de resistencia: a) diente normal; b) centro de resistencia desplazado hacia apical a causa de la disminución ósea; c) con acortamiento radicular; d) diente multirradicular |
Centro de resistencia
Es el punto de un cuerpo (diente) sobre el que una fuerza única producirá traslación, sin inclinación.
El centro de resistencia de un diente no es identificable con facilidad; no obstante, los estudios analíticos determinaron que el centro de resistencia para dientes unirradiculares, con nivel normal del hueso alveolar, se sitúa entre 1/4 y 1/3 de la distancia desde la unión amelocementaria hasta el ápice. Para los dientes multirradiculares está aproximadamente 1 o 2 mm apical de la bifurcación o trifurcación (Figura 1).
Representaremos las fuerzas aplicadas en ortodoncia mediante vectores. Un vector quedará definido por su magnitud, línea de acción, sentido y punto de aplicación. Nos interesará conocer, cuando actúan varias fuerzas, la resultante y su línea de acción. La determinación cuantitativa de las resultantes requiere cálculos trigonométricos.
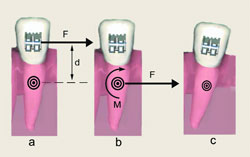 |
| Figura 2. a) La fuerza F aplicada no pasa por el centro de resistencia por lo que se produce un momento de fuerza. b) Resultante en el centro de resistencia. c) Como resultado provocamos una inclinación no deseada además de un movimiento lineal |
Momento de una fuerza
Generalmente la aplicación de la fuerza no se produce a través del centro de resistencia del diente, con lo que se provoca un momento de fuerza, que además del movimiento lineal, también produce un movimiento rotacional o de inclinación. El valor del momento de fuerzas, es el producto de la magnitud esa fuerza (F) por la distancia (d) perpendicular de la línea de acción hasta el centro de resistencia del diente (Figura 2).
Para desarrollar aparatos efectivos y eficaces, es necesario determinar el momento de la fuerza, es decir, tener en consideración la fuerza y la distancia. De esta manera el clínico puede obtener los sistemas de fuerzas deseados, manipulando la magnitud de la fuerza o la distancia a la que actúa la fuerza respecto al centro de resistencia.
La aplicación de fuerzas en el bracket (alambres, resortes y elásticos) genera también el momento de una fuerza; este momento es igual a la magnitud de la fuerza, multiplicada por la distancia desde el punto de aplicación hasta el centro de resistencia.
El sistema de fuerzas resultante describe el movimiento esperado del diente.
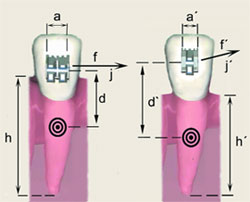 |
| Figura 3. Factores que determinan la ubicación del centro de rotación |
Movimiento de traslación
También se conoce como movimiento “en masa” o traslación pura.
La traslación de un diente, ocurre cuando el ápice radicular y la corona se desplazan igual distancia y en la misma dirección horizontal. La resultante de la fuerza aplicada pasará por el centro de resistencia y el centro de rotación se localiza en el infinito.
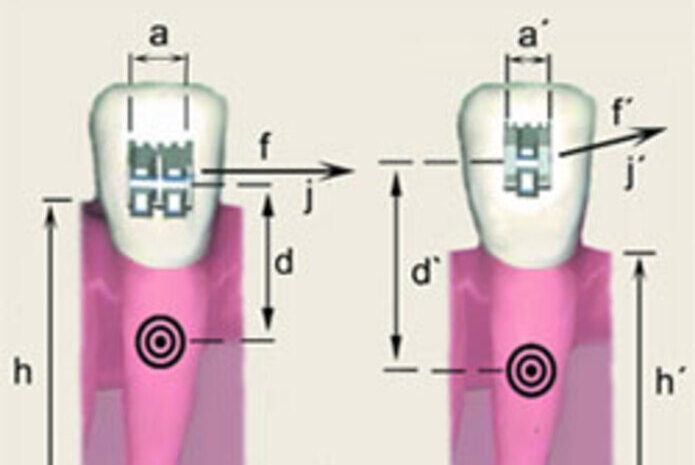
Donde esté situado el centro de rotación, dependerá de la distancia entre el punto de aplicación de la fuerza y el centro de resistencia (Figura 3), es decir:
— De la posición de bracket respecto al centro de resistencia (d, d´).
— De la longitud de la ranura de bracket (a, a´).
— De la resistencia de las estructuras periodontales (h, h´).
— De la magnitud de la fuerza aplicada (f, f´).
— De la dirección de la línea de acción de la fuerza (j, j´).
Para contrarrestar la tendencia a la rotación, producida por una fuerza lineal aplicada sobre el bracket, es decir, para contrarrestar su momento, tendremos que incluir en el sistema un par de fuerzas cuyo momento sea igual, pero dirección contraria de la fuerza.
El par de fuerzas, es el único sistema de fuerzas capaz de producir rotación pura y su efecto es independiente del punto de aplicación sobre el diente.
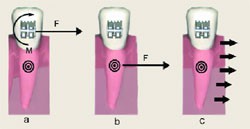 |
| Figura 4. Movimiento en masa: a) la fuerza lineal (F) y momento del par de fuerzas (M) de valor adecuados aplicados, b) tiene como resultante la fuerza F que pasa por el centro de resistencia, c) lo que provoca movimiento de traslación en masa del diente |
Los elementos que encontraremos en el centro de resistencia, inicialmente serían:
— La fuerza.
— El momento de la fuerza.
— El momento del par de fuerzas.
Si al resolverse el momento de la fuerza y el momento del par de fuerzas se anulan mutuamente, el único efecto resultante sería la fuerza. Por ello el movimiento sería “en masa”, traslación pura.
Es decir, para conseguir este movimiento de traslación en masa, debemos lograr que la resultante en el centro de resistencia del diente sea únicamente una fuerza lineal. Para ello, el sistema de fuerzas estará compuesto por una fuerza lineal y un par de fuerzas, cuyo momento tenga sentido contrario y la misma magnitud que el momento de la fuerza (Figura 4).
Movimiento de traslación mediante brazo de potencia
Las palancas auxiliares para el movimiento de traslación no son nuevas en ortodoncia. En 1921 Calvin Case refirió las extensiones soldadas a las bandas, como “brazos de potencia”, y en su honor se mantiene este nombre.
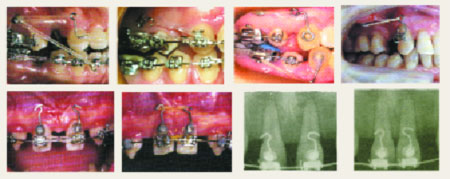 |
| Figura 5. Ejemplos de utilización del gancho de potencia |
El brazo de potencia o gancho de potencia es habitualmente utilizado para conseguir un movimiento de traslación en masa de los dientes, ya que podemos lograr que la fuerza aplicada pase por el centro de resistencia (Figura 5).
En la práctica clínica se obtienen muy buenos resultados para este tipo movimientos mesio-distales, cuando el gancho de potencia utilizado, es de longitud adecuada y esta es adaptable según el caso a tratar. De esta forma, la fuerza pasará por el centro de resistencia del diente a desplazar, y con fuerzas más suaves obtendremos el desplazamiento deseado (Figura 6).
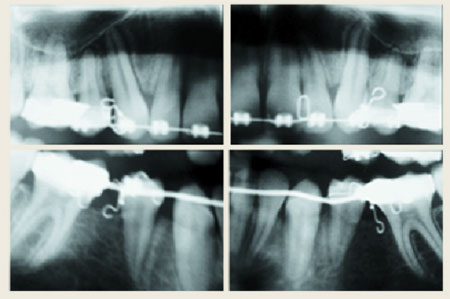 |
| Figura 6. Ejemplos de distalización en masa mediante ganchos de potencia del 13, 23, 34, 44 |
 |
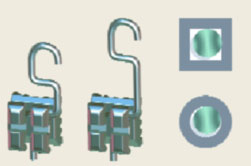 |
| Figura 7. Ejemplos de brackets con brazos de potencia soldados | Figura 8. Nosotros utilizamos el bracket con longitud del brazo de potencia ajustable y con agujero vertical, no ranura, para mejor ajuste |
La longitud óptima del brazo de potencia para cada tipo de diente, es la distancia desde la ranura del bracket al centro de resistencia, menos la longitud mesiodistal de la ranura del bracket (Figura 9).
Igualmente, el movimiento es más eficaz cuando el gancho de potencia pasa por la ranura vertical del bracket, al estar situada el la parte media de mismo, logrando mejor transmisión de fuerzas.
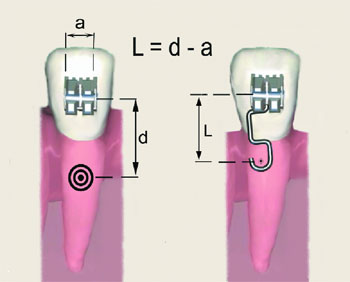 |
| Figura 9. Longitud óptima del brazo de potencia |
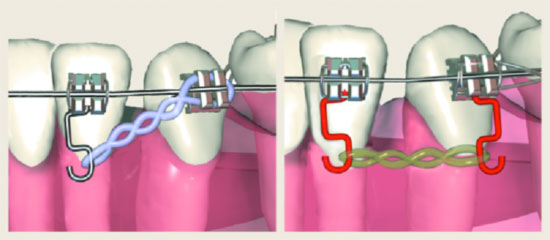 |
| Figura 10. Movimiento de traslación, mediante el empleo de brackets con agujero vertical, alambre fino y duro, conjuntamente con ganchos de potencia adecuados que permiten que la fuerza resultante pase por el centro de resistencia del diente y por lo tanto el diente se desplace en masa con fuerzas ligeras puesto que el grado de fricción entre arco y ranura horizontal es bajo |
 |
 |
 |
 |
 |
 |
 |
 |
| Figura 12u |
Caso clínico 1
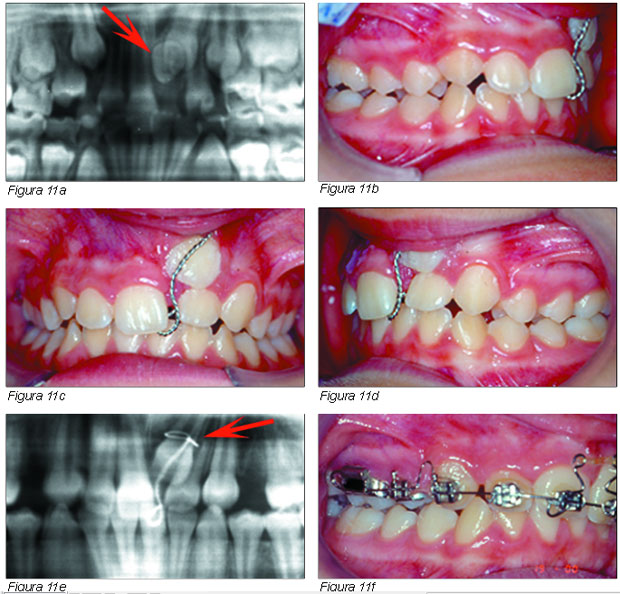
Obsérvese en la Figura 11a la presencia de un supernumerario que impide la erupción del 21.
Las Figuras 11b, 11c y 11d muestran la colocación de una ligadura metálica, para poder extraer el 21.
En la panorámica de la Figura 11e se muestra la colocación de la ligadura metálica, en el 21, y la extracción del 14 y 24.
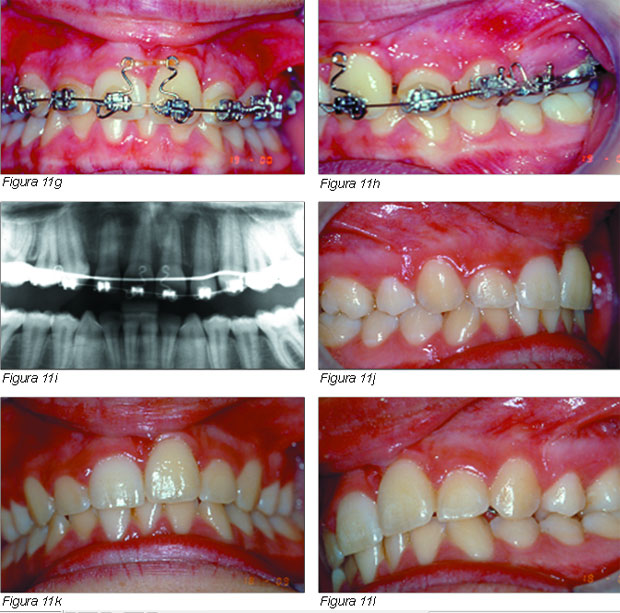
Las Figuras 11f, 11g, y 11h muestran el 21 llevado a su posición normal.
La panorámica de la Figura 11i muestra el 21 en su posición correcta con su inclinación radicular y sin reabsorción radicular.
Caso terminado (Figuras 11j, 11k, 11l).
Caso clínico 2
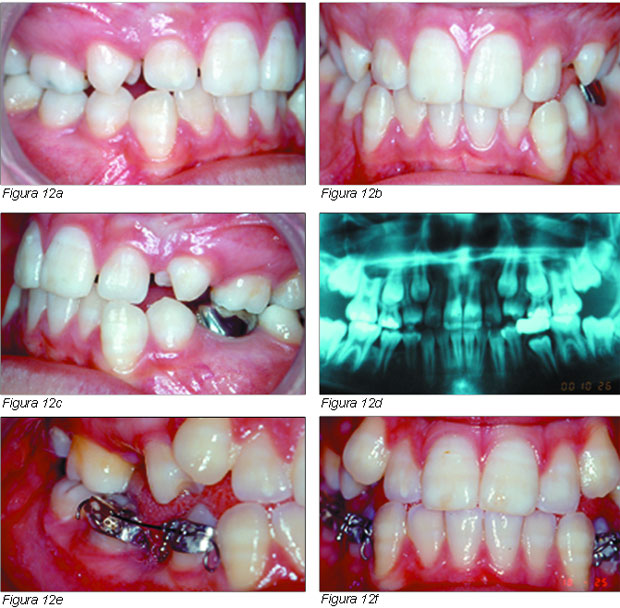
Obsérvese en las Figuras 12a, 12b, 12c y 12d la falta de espacio para los caninos superiores.
Extracción del 15, 25, 35 y 45. Seccionales inferiores (Figuras 12e, 12f, y 12g).
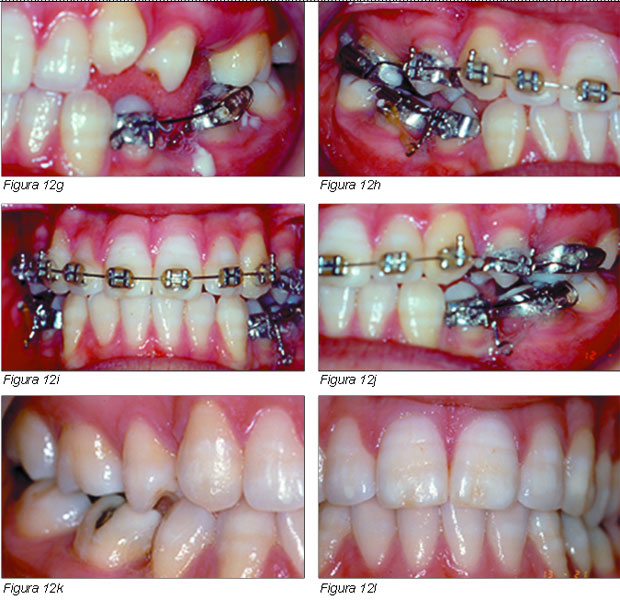
AMS de nivelación, seccionales inferiores con ganchos de potencia en 34 y 44 y cadenas elásticas, Figuras 12h, 12i y 12j.
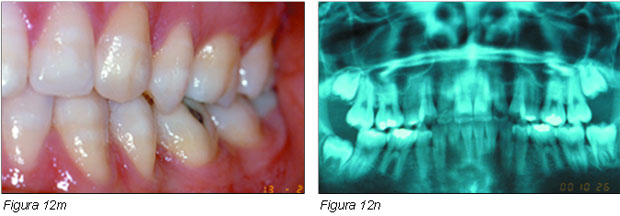
Las Figuras 12k, 12l y 12m muestran el caso finalizado. En la panorámica de la Figura 12n se observa la correcta inclinación radicular y espacio para la erupción de los cordales.
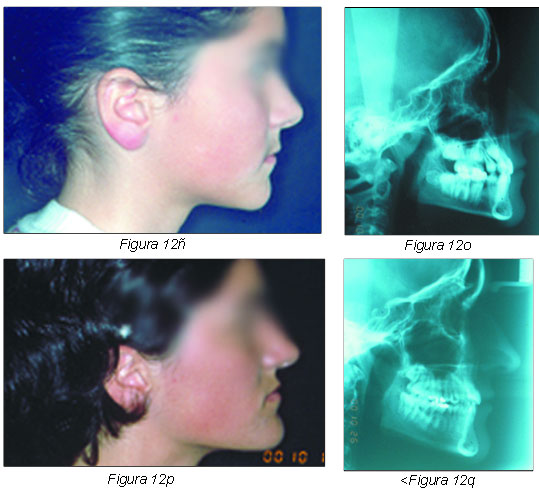
Obsérvese la mejora del perfil, a pesar de las extracciones gracias a las barras palatina y lingual (Figuras 12ñ, 12o, 12p y 12q).
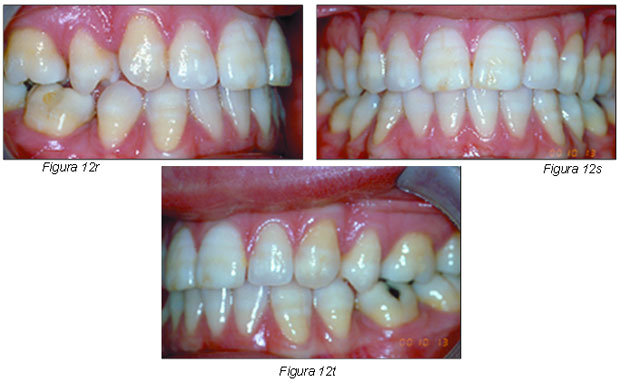
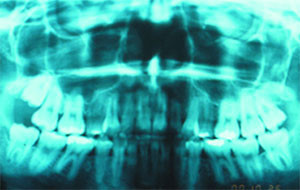
Dos años después, el caso permanece estable y se observa la erupción del 38 y 48 (Figuras 12 r-u).
Bibliografía
Biomecánica
1. A.A. Gianelly and H.M. Goldman. Biologic basis of orthodontics. Lea & Feliger 1971.
2. Horowttz and Hixon. The nature of orthodontic diagnosis. Mosby 1966
3. M.R. Marcotte. Biomecánica en ortodoncia. Masson – Salvat, 1992
4. L.A. Norton and CJ. Burstone. The biology of tooth movement. Crc Press 1986.
5. R.C. Thurow. Atlas de principios ortodonticos. Intermedio 1979.
Técnicas de tratamiento en ortodoncia
1. L.F. Andrews. Coordinator: Julie Olfe. Straightwire the concept and appliance.. La Jalla C.A. 92037 1989.
2. Ortodoncia de Begg. Teoría y técnica. Revista de occidente Madrid 1973.
3. J.C. Bennet – R.P Mc Laughiin. Mecánica en el tratamiento de ortodoncia y la aparatología de arco recto. Wolfe1994.
4. Ehchiro Nakajima. Introduction to bioprogresive therapy. Quintessence1987.
5. J. Garriere. La técnica de anclaje inverso y su ecuación. Quintessence 1990.
6. Técnica bioprogresiva de Ricketts. Medica Panamericana 1983
7. Ch.Tweed. Clinical orthodontics. Mosby 1966.
Articulos
1. Carano A.; Velo S.; Leone, P.; Siciliani, G. Clinical applications of the miniscrew anchorage system. J. Clin. Orthod. 39:9-24,2005.
2. Chang, D.R.; Chun Y.S. Use bonded power anns in cases with missing upper lateral incisors. J.Clin. Orthod. 38:539-542,2004.
3. Mah, J.; Bergstrand, F. Temporary anchorage devices: Astatus report J. Clin. Orrthod. 39:132-136,2005.
4. Mulligan T.F. Common sense Mechanics 1 J Clin Orthod 1979; 13:588-94.
5. Mulligan T.F. Common sense Mechanics 2 J Clin Orthod 1979; 13:676-73.
6. Mulligan T.F. Common sense Mechanics 3 Static Equilibrium J Clin Orthod 197913; 762-66
7. Mulligan T.F. Common sense Mechanics 4 Overlays J Clin Orthod 1979 13; 808-15.
8. Mulligan T.F. Common sense Mechanics 6 Tip-back J Clin Orthod. 1980; 14:180-89.
9. Mulligan T.F. Common sense Mechanics 7 Differential Torque 1980; 14:180-89.
10. Mulligan T.F. Common sense Mechanics 8 Wire/Bracket Relation J Clin Orthod 1980:265-72.
11. Mulligan T.F. Common sense Mechanics 9 Cuspid Retractíon J Clin Orthod 1980:336-42.
12. Mulligan T.F. Common sense Mechanics 10 Extractíon Mechanics J Clin Orthod 1980:12-23.
13. Mulligan T.F. Common sense Mechanics 11 Extractíon Mechanics J Clin Orthod 1980:481-
14. Mulligan T.F. Common sense Mechanics 12 Total Treatment J Clin Orthod 1980:546-53.
15. Mulligan T.F. Common sense Mechanics 13 Total Treatment J Clin Orthod 1980:637-47.
16. Mulligan T.F. Common sense Mechanics 14 Class III J Clin Orthod 1980; 14:716-23.
17. Mulligan T.F. Common sense Mechanics 15 Anterior crossbites J Clin Orthod 1980:788-95.
18. Mulligan T.F. Common sense Mechanics 16 Questions/Answers J Clin Orthod 1980: 855-68.
19. Park, Y.C.; Chu, J.H.; Choi, Y.J.; Choi, N.C. Extraction space closure with vacuum-fonned splints and miniscrew anchorage. J.Clin. Orthod. 39:76-79,2005.
20. Ricketts RM. Bench RW. Gugino CF. Alto Bioprogressive Therapy. Book 1. Denver. CO. Rocky Mountain Orthodontícs 1979; 93-126.
21. Ricketts RM. Bench RW. Gugino CF. Alto Bioprogressive Therapy. Book 1. Denver. CO. Rocky Mountain Orthodontícs 1979; 93-126.